
Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
Взаимное расположение двух линий
Для того чтобы определить взаимное расположение двух линий, надо знать уравнения этих линий. Если система этих уравнений имеет решения, то линии имеют общие точки. В противном случае общих точек нет. Число общих точек равно числу решений системы уравнений.
Линии первого порядка (алгебраические линии первого порядка – это прямые линии. Рассматриваются задачи: через заданную на плоскости точку М прямую с угловым коэффициентом k; провести прямую через две заданные точки А и В; найти угол между прямыми через угловые коэффициенты этих прямых; условие параллельности и условие перпендикулярности двух прямых).
Пусть дана прямая L на координатной плоскости Оху.
Определение. Углом наклона прямой к оси абсцисс называется угол поворота оси абсцисс вокруг любой ее точки против часовой стрелки до положения параллельности (или совпадения) с данной прямой.
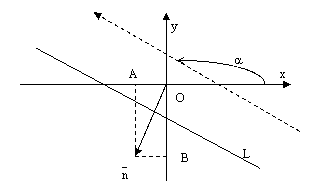
рис.1.
Из определения следует, что угол наклона  прямой L к оси Ох может изменяться от нуля до
прямой L к оси Ох может изменяться от нуля до  :
: 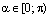 . Если прямая
. Если прямая 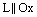 , то
, то  .
.
Пусть
 (1)
(1)
– общее уравнение прямой L, где 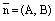 – нормальный вектор прямой L и
– нормальный вектор прямой L и  . Тогда
. Тогда  и
и  (см. рис.1). Выразим у из уравнения (1)
(см. рис.1). Выразим у из уравнения (1)
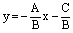 .
.
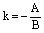 ,
,  .
.
Уравнение прямой L принимает вид:
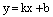 .
.
Определение. Уравнение прямой вида
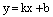 (2)
(2)
называется уравнением прямой с угловым коэффициентом, а коэффициент k называется угловым коэффициентом данной прямой.
Теорема. В уравнении прямой с угловым коэффициентом
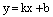
угловой коэффициент k равен тангенсу угла наклона прямой к оси абсцисс:
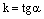 . (3)
. (3)
Доказательство. 1) Если прямая 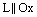 , то
, то  и
и 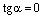 . С другой стороны, ее нормальный вектор
. С другой стороны, ее нормальный вектор  и
и 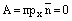 .
.
Тогда  и, следовательно,
и, следовательно, 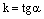 , ч.т.д.
, ч.т.д.
2) Пусть 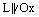 , тогда
, тогда 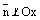 ,
,  и
и 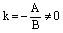 . Пусть F – точка пересечения прямой L с осью абсцисс. Тогда
. Пусть F – точка пересечения прямой L с осью абсцисс. Тогда
 ,
,  .
.
Опишем окружность единичного радиуса с центром в точке F , а в точке оси Ох с координатой  проведем касательную m к этой окружности. См. рис.2.
проведем касательную m к этой окружности. См. рис.2.

рис.2.
Выберем положительное направление на прямой m, так, чтобы 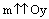 . Тогда ось m является осью тангенсов для данной единичной (тригонометрической) окружности.
. Тогда ось m является осью тангенсов для данной единичной (тригонометрической) окружности.
Пусть Р – точка пересечения прямой L с осью тангенсов m. Тогда, с одной стороны,  , где
, где  – угол наклона прямой L к оси Ох, а, с другой стороны, точка
– угол наклона прямой L к оси Ох, а, с другой стороны, точка 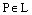 и
и  , откуда и следует равенство
, откуда и следует равенство 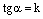 , ч.т.д.
, ч.т.д.
Теорема доказана.
Заметим, что приведенное доказательство принадлежит автору этих лекций. Достоинством этого доказательства является то, что оно не зависит ни от величины угла наклона  , ни от величины коэффициента
, ни от величины коэффициента  .
.
В заключение отметим, что коэффициент b в уравнении (2) равен величине отрезка, отсекаемого прямой от оси ординат (см. рис.2).
44. Уравнение в прямой в  , проходящей через точку перпендикулярную вектору.
, проходящей через точку перпендикулярную вектору.
Линия на плоскости является прямой тогда и только тогда, когда она является алгебраической линией первого порядка.
Доказательство. Необходимость. Пусть l − прямая на плоскости, прходящая через точку M0 и параллельная ненулевому вектору а. Пусть Oxy − произвольная аффинная система координат и а = {m, n}, М0(x0, y0). Тогда прямая l описывается каноническим уравнением (5.2.2) или, что то же самое, уравнением n(x - x0) - m(y - y0) = 0, которое, если положить А = n, B = -m, C = -n x0 + my0, может быть записано в виде
Ax + By + C = 0. (5.2.6)
Так как вектор а = {m, n} ≠ 0, то по крайней мере один из коэффициентов А или В отличен от нуля. Поэтому левая часть уравнения (5.2.6) представляет собой алгебраический многочлен первой степени. Следовательно, любая прямая на плоскости является алгебраической линией первого порядка.
Достаточность. Пусть в аффинной системе координат Oxy линия l определяется уравнением (5.2.6). Это уравнение имеет частное решение
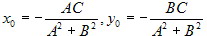 , ибо Ax0 + By0 + C ≡ 0
, ибо Ax0 + By0 + C ≡ 0
Вычитая последнее равенство из (5.2.6), получим, что А(x - x0) + В(y - y0) = 0 или, что то же самое,

В силу теоремы 5.2 это уравнение определяет прямую, проходящую через точку М0(x0, y0), с направляющим вектором а = {-В, А}. Теорема доказана.
Уравнение (5.2.6) называется общим уравнением прямой на плоскости. Вектор n = {A, B} называется вектором нормали к прямой относительно уравнения (5.2.6).
Общее уравнение прямой называется полным, если все коэффициенты А, В, С отличны от нуля.
Теорема 5.4. В аффинной системе координат Oxy на плоскости вектор а = {m, n}, параллелен прямой, заданной общим уравнением (5.2.6), тогда и только тогда, когда
Am + Bn = 0, (5.2.7)
Доказательство. Как следует из доказательства теоремы 5.3, вектор b = {-В, А} является направляющим вектором прямой. Это означает, что вектор а параллелен этой прямой тогда и только тогда, когда а коллинеарен b, т.е. когда

или, что то же самое, Am + Bn = 0. Теорема доказана.
Замечание 2. Левые части условия (5.2.7) можно рассматривать как скалярные произведения вектора нормали n и вектора а в ортонормированном базисе. Таким образом, в прямоугольной декартовой системе координат вектор нормали n = {A, B} к прямой (5.2.6) перпендикулярен этой прямой.
Уравнение в отрезках. Полное уравнение (5.2.6) прямой на плоскости может быть записано в следующем виде:

Полагая а = - С/А, b = - C/B, получим эквивалентное уравнение
 ,
,
называемое уравнениями прямой в отрезках. Числа а, b в этом уравнении имеют простой геометрический смысл (рис. 2): они равны величинами отрезков, которые отсекает прямая на осях координат.

Векторное уравнение. 1. Параметрическое уравнение (5.2.4) представляет собой векторное уравнение прямой на плоскости через направляющий вектор. Оно порождает другие формы векторных уравнений прямой. Это уравнение означает компланарность векторов r - r0 и а, что согласно критерию компланарности
(теорема 4.7) равносильно равенству
( r - r0, а) = 0 (5.2.8)
или, в силу линейности смешанного произведения,
(r, а) = С (5.2.9)
где С − константа, равная (r0, а).
2. Из аксиом геометрии следует, что на плоскости через заданную точку проходит единственная прямая, перпендикулярная заданному вектору.
Теорема 5.5. Уравнение прямой на плоскости, проходящей через точку М0(r0) перпендикулярно вектору n, имеет вид
( r - r0, n) = 0, (5.2.10)
или, что то же самое,
( r, n) = D, (5.2.11)
где D − константа, равная (r0, n).
Доказательство. Утверждение теоремы вытекает из того, что точка M(r) лежит на прямой тогда и только тогда, когда векторы  и n ортогональны. Теорема доказана.
и n ортогональны. Теорема доказана.
45. Уравнение прямой в  , проходящей через точку перпендикулярно вектору.
, проходящей через точку перпендикулярно вектору.
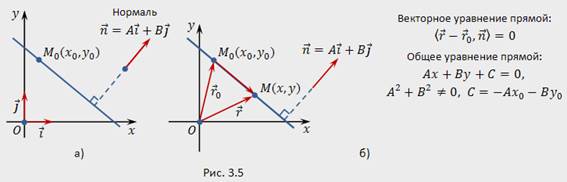
Требуется составить уравнение прямой, проходящей через точку  перпендикулярно вектору
перпендикулярно вектору  .
.
Выберем на плоскости произвольную точку  . Обозначим
. Обозначим  и
и  — радиус-векторы точек
— радиус-векторы точек  и
и  . Точка
. Точка  принадлежит заданной прямой тогда и только тогда, когда векторы
принадлежит заданной прямой тогда и только тогда, когда векторы  и
и  перпендикулярны (рис.3.5,б). Условие ортогональности запишем при помощи скалярного произведения:
перпендикулярны (рис.3.5,б). Условие ортогональности запишем при помощи скалярного произведения:
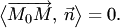
Учитывая, что 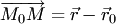 , получаем векторное уравнение прямой:
, получаем векторное уравнение прямой:
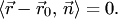
| (3.5) |
Это уравнение можно записать в другой форме. Преобразуем левую часть , используя свойства скалярного произведения. Обозначая  , получаем уравнение
, получаем уравнение

| (3.6) |
выражающее постоянство проекций на нормаль  радиус-векторов точек, принадлежащих прямой.
радиус-векторов точек, принадлежащих прямой.
Получим координатную форму записи векторного уравнения прямой (3.5). Так как  и
и  , по формуле (1.9) находим
, по формуле (1.9) находим  или
или
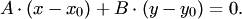
| (3.7) |
Полученное соотношение (3.7) позволяет по координатам точки  и координатам
и координатам  нормали
нормали  записать уравнение прямой без промежуточных вычислений.
записать уравнение прямой без промежуточных вычислений.
46. Уравнение прямой, проходящей через две точки. Уравнение прямой в  , в отрезках на осях координат.
, в отрезках на осях координат.
Пусть в пространстве заданы две точки M 1 ( x 1 , y 1 , z 1 ) и M2 ( x 2, y 2 , z 2 ), тогда уравнение прямой, проходящей через эти точки:

Если какой- либо из знаменателей равен нулю, следует приравнять нулю соответствующий числитель.На плоскости записанное выше уравнение прямой упрощается:
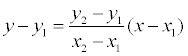
если х 1 ≠ х2 и х = х 1 , если х 1 = х2 .
Дробь  = k называется угловым коэффициентом прямой.
= k называется угловым коэффициентом прямой.


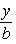

 (3)
(3)
где a - величина отрезка, отсекаемого прямой на оси Ox; b - величина отрезка, отсекаемого прямой на оси Oy.
Каждый из этих отрезков отложен от начала координат.
Особенности этого уравнения такие: в левой части уравнения между дробями сосит знак плюс, величины a и b могут быть как положительными, так и отрицательными, правая часть уравнения равна единице.
Последнее изменение этой страницы: 2016-07-22
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...