
Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
Элементы теории графов. Цикл Гамильтона
Пусть задано некоторое непустое множество Х множество, состоящее из пар элементов множества X. Пары во множестве могут повторяться, и также могут повторяться элементы в парах. Множества Х задают граф 0=(Х, Y) [10: с. 12].
Элементы множества называют вершинами графа, элементы множества V — ребрами графа.
Если пары во множестве V повторяются, то граф С называют псевдографом или графом с кратными ребрами.
Если элементы в парах множества не упорядочены, то граф С называют неориентированным графом. Если они упорядочены, то граф О является ориентированным графом или орграфом, а элементы множества V называют дугами.
Графически граф задается в виде точек и линий, их соединяющих.
Введем ряд основных понятий для неориентированного графа. Ребро, начало и конец которого совпадают, называется петлей. Вершины называются смежными или соседними, если существует ребро, их соединяющее.
Если вершина является началом или концом ребра, то вершина и ребро называются инцидентными.
Степенью вершины называется число инцидентных ей ребер. Вершина, степень которой равна нулю, называется изолированной. Вершина, степень которой равна единице, называется висячей или тупиковой.
Маршрутом в графе называется последовательность вершин и ребер, в которой конец предыдущего ребра совпадает с началом следующего), это не относится к первому и последнему ребру). Число ребер в маршруте определяет его длину.
Цепью называется маршрут, в котором все ребра попарно различны.
Простой называется цепь, в которой все вершины попарно различны.
Циклом (простым циклом) называется цепь (простая цепь), начало и конец которой совпадают.
Граф называется связным, если для любых двух его вершин существует цепь, соединяющая эти вершины.
Расстоянием между вершинами связного графа называется длина самой короткой цепи, соединяющей вершины.
Диаметром графа называется максимальное расстояние между его вершинами.
Деревом называется связный граф без циклов
Граф называется регулярным степени i, если все его вершины имеют степень i.
Граф называется полным, если любые две его вершины соединены ребром. Лесом называется граф без циклов, т.е. совокупность деревьев.
Регулярный граф, все вершины которого имеют степень 1, называется паросочетанием. Граф называется двудольным, если множество его вершин X может быть разделено на два непересекающихся подмножества таким образом, что каждое ребро графа соединяет вершины из двух разных подмножеств[9: с. 36].
Гамильтонов граф — в теории графов это граф, содержащий гамильтонову цепь или гамильтонов цикл.
Гамильтонов путь (или гамильтонова цепь) — путь (цепь), содержащий каждую вершину графа ровно один раз. Гамильтонов путь, начальная и конечная вершины которого совпадают, называется гамильтоновым циклом. Гамильтонов цикл является простым остовным циклом.
Гамильтоновы путь, цикл и граф названы в честь ирландского математика У. Гамильтона, который впервые определил эти классы, исследовав задачу «кругосветного путешествия» по додекаэдру, узловые вершины которого символизировали крупнейшие города Земли, а рёбра — соединяющие их дороги. В ориентированном графе каждая дуга имеет направление, показанное стрелкой
Маршрут в ориентированном графе часто называют контуром, а цепь — путем.
Постановка задачи коммивояжера
Задача коммивояжера (в дальнейшем сокращённо - ЗК) является одной из знаменитых задач теории комбинаторики. Она была поставлена в 1934 году, и об неё, как об Великую теорему Ферма обламывали зубы лучшие математики. В своей области (оптимизации дискретных задач) ЗК служит своеобразным полигоном, на котором испытываются всё новые методы.
Постановка задачи следующая.
Коммивояжер (бродячий торговец) должен выйти из первого города, посетить по разу в неизвестном порядке города 2,1,3..n и вернуться в первый город. Расстояния между городами известны. В каком порядке следует обходить города, чтобы замкнутый путь (тур) коммивояжера был кратчайшим?
Чтобы привести задачу к научному виду, введём некоторые термины. Итак, города перенумерованы числами jÎТ=(1,2,3..n). Тур коммивояжера может быть описан циклической перестановкой t=(j1,j2,..,jn,j1), причём все j1..jn – разные номера; повторяющийся в начале и в конце j1,показывает, что перестановка зациклена. Расстояния между парами вершин Сijобразуют матрицу С. Задача состоит в том, чтобы найти такой тур t, чтобы минимизировать функционал[2: с. 280]

| (1) |
Относительно математизированной формулировки ЗК уместно сделать два замечания.
Во-первых, в постановке Сijозначали расстояния, поэтому они должны быть неотрицательными, т.е. для всех jÎТ:
| Сij³0; Cjj=∞ | (2) |
(последнее равенство означает запрет на петли в туре), симметричными, т.е. для всех i,j:
| Сij= Сji. | (3) |
и удовлетворять неравенству треугольника, т.е. для всех:
| Сij+ Сjk³Cik | (4) |
В математической постановке говорится о произвольной матрице. Сделано это потому, что имеется много прикладных задач, которые описываются основной моделью, но всем условиям (2)-(4) не удовлетворяют. Особенно часто нарушается условие (3) (например, если Сij – не расстояние, а плата за проезд: часто туда билет стоит одну цену, а обратно – другую). Поэтому мы будем различать два варианта ЗК: симметричную задачу, когда условие (3) выполнено, и несимметричную - в противном случае. Условия (2)-(4) по умолчанию мы будем считать выполненными [13: с. 68].
Второе замечание касается числа всех возможных туров. Внесимметричной ЗК все туры t=(j1,j2,..,jn,j1) и t’=(j1,jn,..,j2,j1) имеют разную длину и должны учитываться оба. Разных туров очевидно (n-1)!.
Зафиксируем на первом и последнем месте в циклической перестановке номер j1, а оставшиесяn-1 номеров переставим всеми (n-1)! возможными способами. В результате получим все несимметричные туры. Симметричных туров имеется в два раз меньше, т.к. каждый засчитан два раза: как t и как t’.
Можно представить, что С состоит только из единиц и нулей. Тогда С можно интерпретировать, как граф, где ребро (i,j) проведено, если Сij=0 и не проведено, если Сij=1. Тогда, если существует тур длины 0, то он пройдёт по циклу, который включает все вершины по одному разу. Такой цикл называется гамильтоновым циклом. Незамкнутый гамильтонов цикл называется гамильтоновой цепью (гамильтоновым путём).
В терминах теории графов симметричную ЗК можно сформулировать так:
Дана полная сеть с n вершинами, длина ребра (i,j)=Сij. Найти гамильтонов цикл минимальной длины.
В несимметричной ЗК вместо «цикл» надо говорить «контур», а вместо «ребра» - «дуги» или «стрелки».
Некоторые прикладные задачи формулируются как ЗК, но в них нужно минимизировать длину не гамильтонова цикла, а гамильтоновой цепи. Такие задачи называются незамкнутыми. Некоторые модели сводятся к задаче о нескольких коммивояжерах, но мы здесь их рассматривать не будем.
Методы решения ЗК
Жадный алгоритм
Жадный алгоритм – алгоритм нахождения наикратчайшего расстояния путём выбора самого короткого, ещё не выбранного ребра, при условии, что оно не образует цикла с уже выбранными рёбрами. «Жадным» этот алгоритм назван потому, что на последних шагах приходится жестоко расплачиваться за жадность [3: с. 172].

Рис. 1
Посмотрим, как поведет себя при решении ЗК жадный алгоритм. Здесь он превратится в стратегию «иди в ближайший (в который еще не входил) город». Жадный алгоритм, очевидно, бессилен в этой задаче. Рассмотрим для примера сеть на рис. 1, представляющую узкий ромб. Пусть коммивояжер стартует из города 1. Алгоритм «иди вы ближайший город» выведет его в город 2, затем 3, затем 4; на последнем шаге придется платить за жадность, возвращаясь по длинной диагонали ромба. В результате получится не кратчайший, а длиннейший тур.
В пользу процедуры «иди в ближайший» можно сказать лишь то, что при старте из одного города она не уступит стратегии «иди в дальнейший».
Как видим, жадный алгоритм ошибается. Можно ли доказать, что он ошибается умеренно, что полученный им тур хуже минимального, положим, в 1000 раз? Мы докажем, что этого доказать нельзя, причем не только для жадного логарифма, а для алгоритмов гораздо более мощных. Но сначала нужно договориться, как оценивать погрешность неточных алгоритмов, для определенности, в задаче минимизации. Пусть fB- настоящий минимум, а fA - тот квазиминимум, который получен по алгоритму. Ясно, чтоfA/fB≥1, но это – тривиальное утверждение, что может быть погрешность. Чтобы оценить её, нужно зажать отношение оценкой сверху:
| fA/fB ≥1+ nε, | (5) |
где, как обычно в высшей математике, ε≥0, но, против обычая, может быть очень большим. Величина ε и будет служить мерой погрешности. Если алгоритм минимизации будет удовлетворять неравенству (5), мы будем говорить, что он имеет погрешность ε.
Предположим теперь, что имеется алгоритм А решения ЗК, погрешность которого нужно оценить[15: с. 46]. Возьмем произвольный граф G (V,E) и по нему составим входную матрицу ЗК:
| С[i,j]={ | 1,если ребро (i,j) принадлежит Е |
| 1+nε в противном случае |
Если в графе G есть гамильтонов цикл, то минимальный тур проходит по этому циклу и fB = n. Если алгоритм А тоже всегда будет находить этот путь, то по результатам алгоритма можно судить, есть ли гамильтонов цикл в произвольном графе. Однако, непереборного алгоритма, который мог бы ответить, есть ли гамильтонов цикл в произвольном графе, до сих пор никому не известно. Таким образом, наш алгоритм А должен иногда ошибаться и включать в тур хотя бы одно ребро длины 1+nε. Но тогда fA³(n-1)+(1+nε) так что fA/fB=1+nε т.е. превосходит погрешность ε на заданную неравенством (5). О величине ε в нашем рассуждении мы не договаривались, так что ε может быть произвольно велик.
Таким образом, доказана следующая теорема [8: с.143].
Либо алгоритм А определяет, существует ли в произвольном графе гамильтонов цикл, либо погрешность А при решении ЗК может быть произвольно велика.
Это соображение было впервые опубликовано Сани и Гонзалесом в 1980 г. Теорема Сани-Гонзалеса основана на том, что нет никаких ограничений на длину ребер. Теорема не проходит, если расстояния подчиняются неравенству треугольника (4).

Рис. 2
Если оно соблюдается, можно предложить несколько алгоритмов с погрешностью 12. Прежде, чем описать такой алгоритм, следует вспомнить старинную головоломку. Можно ли начертить одной линией открытый конверт? Рис.2 показывает, что можно (цифры на отрезках показывают порядок их проведения). Закрытый конверт (рис. 2.) одной линией нарисовать нельзя и вот почему. Будем называть линии ребрами, а их перекрестья – вершинами.
Когда через точку проводится линия, то используется два ребра – одно для входа в вершину, одно – для выхода. Если степень вершины нечетна – то в ней линия должна начаться или кончиться. На рис. 2 вершин нечетной степени две: в одной линия начинается, в другой – кончается. Однако на рис. 4 имеется четыре вершины степени три, но у одной линии не может быть четыре конца. Если же нужно прочертить фигуру одной замкнутой линией, то все ее вершины должны иметь четную степень.
Верно и обратное утверждение: если все вершины имеют четную степень, то фигуру можно нарисовать одной незамкнутой линией. Действительно, процесс проведения линии может кончиться, только если линия придет в вершину, откуда уже выхода нет: все ребра, присоединенные к этой вершине (обычно говорят: инцидентные этой вершине), уже прочерчены. Если при этом нарисована вся фигура, то нужное утверждение доказано; если нет, удалим уже нарисованную часть G’. После этого от графа останется одна или несколько связных компонент; пусть G’ – одна из таких компонент. В силу связности исходного графа G, G’ и G’’ имеют хоть одну общую вершину, скажем, v. Если в G’’ удалены какие-то ребра, то по четному числу от каждой вершины. Поэтому G’’ – связный и все его вершины имеют четную степень. Построим цикл в G’’ (может быть, не нарисовав всего G’’) и через v добавим прорисованную часть G’’ к G’. Увеличивая таким образом прорисованную часть G’, мы добьемся того, что G’ охватит весь G.
Эту задачу когда-то решил Эйлер, и замкнутую линию, которая покрывает все ребра графа, теперь называю эйлеровым циклом. По существу была доказана следующая теорема [12: с. 222].
Эйлеров цикл в графе существует тогда и только тогда, когда (1) граф связный и (2) все его вершины имеют четные степени.
Деревянный алгоритм
Теперь можно обсудить алгоритм решения ЗК через построение кратчайшего остовного дерева. Для краткости будет называть этот алгоритм деревянным.
Вначале обсудим свойство спрямления. Рассмотрим какую-нибудь цепь, например, на рис.5. Если справедливо неравенство треугольника, то d[1,3]£d[1,2]+d[2,3] и d[3,5]£d[3,4]+d[4,5]. Сложив эти два неравенства, получим d[1,3]+d[3,5]£d[1,2]+d[2,3]+d[3,4]+d[4,5]. По неравенству треугольника получим. d[1,5]£d[1,3]+d[3,5]. Окончательно d[1,5]£d[1,2]+d[2,3]+d[3,4]+d[4,5].
Итак, если справедливо неравенство треугольника, то для каждой цепи верно, что расстояние от начала до конца цепи меньше (или равно) суммарной длины всех ребер цепи. Это обобщение расхожего убеждения, что прямая короче кривой.
Вернемся к ЗК и опишем решающий ее деревянный алгоритм.
1. Построим на входной сети ЗК кратчайшее остовное дерево и удвоим все его ребра. Получим граф G – связный и с вершинами, имеющими только четные степени.
2. Построим эйлеров цикл G, начиная с вершины 1, цикл задается перечнем вершин.
3. Просмотрим перечень вершин, начиная с 1, и будем зачеркивать каждую вершину, которая повторяет уже встреченную в последовательности. Останется тур, который и является результатом алгоритма.
Пример 1. Дана полная сеть, показанная на рис.3. Найти тур жадным и деревянным алгоритмами.

Рис. 3
| табл. 1.3.2.1 | ||||||
| - | ||||||
| - | ||||||
| - | ||||||
| - | ||||||
| - | ||||||
| - | ||||||
| - | ||||||
Решение. Жадный алгоритм (иди в ближайший город из города 1) дает тур 1–(4)–3-(3)–5(5)–4–(11)–6–(10)–2–(6)–1, где без скобок показаны номера вершин, а в скобках – длины ребер. Длина тура равна 39, тур показана на рис. 4.
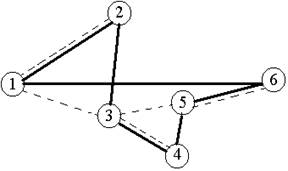
Рис. 4
2. Деревянный алгоритм вначале строит остовное дерево, показанное на рис. 6 штриховой линией, затем эйлеров цикл 1-2-1-3-4-3-5-6-5-3-1, затем тур 1-2-3-4-5-6-1 длиной 43, который показан сплошной линией на рис. 4.
Теорема. Погрешность деревянного алгоритма равна 1.
Доказательство. Возьмем минимальный тур длины fBи удалим из него максимальное ребро. Длина получившейся гамильтоновой цепи LHC меньше fB. Но эту же цепь можно рассматривать как остовное дерево, т. к. эта цепь достигает все вершины и не имеет циклов. Длина кратчайшего остовного дерева LMT меньше или равна LHC. Имеем цепочку неравенств [8: с. 133]
| fB>LHC³LMT | (6) |
Но удвоенное дерево – оно же эйлеров граф – мы свели к туру посредством спрямлений, следовательно, длина полученного по алгоритму тура удовлетворяет неравенству
| 2LMT>fA | (7) |
Умножая (6) на два и соединяя с (7), получаем цепочку неравенств
| 2fB>2LHC³2LMT³fA | (8) |
Т.е. 2fB>fA, т.е. fA/fB>1+e; e=1.
Теорема доказана[8: с. 137].
Таким образом, мы доказали, что деревянный алгоритм ошибается менее, чем в два раза. Такие алгоритмы уже называют приблизительными, а не просто эвристическими.
Известно еще несколько простых алгоритмов, гарантирующих в худшем случае e=1. Для того, чтобы найти среди них алгоритм поточнее, зайдем с другого конца и для начала опишем «brute-forceenumeration» - «перебор животной силой», как его называют в англоязычной литературе. Понятно, что полный перебор практически применим только в задачах малого размера. Напомним, что ЗК с n городами требует при полном переборе рассмотрения (n-1)!/2 туров в симметричной задаче и (n-1)! Туров в несимметричной, а факториал, как показано в следующей таблице, растет удручающе быстро:
| табл. 1.3.2.2 | |||||||||
| 5! | 10! | 15! | 20! | 25! | 30! | 35! | 40! | 45! | 50! |
| ~102 | ~106 | ~1012 | ~1018 | ~10125 | ~1032 | ~1040 | ~1047 | ~1056 | ~1064 |
Чтобы проводить полный перебор в ЗК, нужно научиться (разумеется, без повторений) генерировать все перестановки заданного числа m элементов. Это можно сделать несколькими способами, но самый распространенный (т.е. приложимый для переборных алгоритмов решения других задач) – это перебор в лексикографическом порядке.
Пусть имеется некоторый алфавит и наборы символов алфавита (букв), называемые словами. Буквы в алфавите упорядочены: например, в русском алфавите порядок букв аµбµя (символ µ читается «предшествует)». Если задан порядок букв, можно упорядочить и слова. Скажем, дано слово u=(u1,u2,..,um) – состоящее из букв u1,u2,..,um - и слово v =(v1,v2,..,vb). Тогда если u1µv1, то и uµv, если же u1=v1, то сравнивают вторые буквы и т.д. Этот порядок слов и называется лексикографическим. Поэтому в русских словарях (лексиконах) слово «абажур» стоит раньше слова «абака». Слово «бур» стоит раньше слова «бура», потому что пробел считается предшествующим любой букве алфавита[2: с. 79].
Рассмотрим, скажем, перестановки из пяти элементов, обозначенных цифрами 1..5. Лексикографически первой перестановкой является 1-2-3-4-5, второй – 1-2-3-5-4, …, последней – 5-4-3-2-1. Нужно осознать общий алгоритм преобразования любой перестановки в непосредственно следующую.
Правило такое: скажем, дана перестановка 1-3-5-4-2. Нужно двигаться по перестановке справа налево, пока впервые не увидим число, меньшее, чем предыдущее (в примере это 3 после 5). Это число, Pi-1 надо увеличить, поставив вместо него какое-то число из расположенных правее, от Pi до Pn. Число большее, чем Pi-1, несомненно, найдется, так как Pi-1<Pi . Если есть несколько больших чисел, то, очевидно, надо ставить меньшее из них. Пусть это будет Pj,j>i-1. Затем число Pi-1 и все числа от Pi до Pn, не считая Pj нужно упорядочить по возрастанию. В результате получится непосредственно следующая перестановка, в примере – 1-4-2-3-5. Потом получится 1-4-2-5-3 (тот же алгоритм, но упрощенный случай) и т.д.
Нужно понимать, что в ЗК с n городами не нужны все перестановки из n элементов. Потому что перестановки, скажем, 1-3-5-4-2 и 3-5-4-2-1 (последний элемент соединен с первым) задают один и тот же тур, считанный сперва с города 1, а потом с города 3. Поэтому нужно зафиксировать начальный город 1 и присоединять к нему все перестановки из остальных элементов. Этот перебор даст (n-1)! разных туров, т.е. полный перебор в несимметричной ЗК (мы по-прежнему будем различать туры 1-3-5-4-2 и 1-2-4-5-3).
Пример 2. Решим ЗК, поставленную в Примере 1 лексикографическим перебором. Приведенная выше программа напечатает города, составляющие лучший тур: 1-2-6-5-4-3 и егодлину 36.
Желательно усовершенствовать перебор, применив разум. В следующем пункте описан алгоритм, который реализует простую, но широко применимую и очень полезную идею[3: с. 12].
Метод ветвей и границ
К идее метода ветвей и границ приходили многие исследователи, но Литтл с соавторами на основе указанного метода разработали удачный алгоритм решения ЗК и тем самым способствовали популяризации подхода. С тех пор метод ветвей и границ был успешно применён ко многим задачам, для решения ЗК было придумано несколько других модификаций метода, но в большинстве учебников излагается пионерская работа Литтла[1: с. 22].
Общая идея тривиальна: нужно разделить огромное число перебираемых вариантов на классы и получить оценки (снизу – в задаче минимизации, сверху – в задаче максимизации) для этих классов, чтобы иметь возможность отбрасывать варианты не по одному, а целыми классами. Трудность состоит в том, чтобы найти такое разделение на классы (ветви) и такие оценки (границы), чтобы процедура была эффективной.
Удовлетворительных теоретических оценок быстродействия алгоритма Литтла и родственных алгоритмов нет, но практика показывает, что на современных ЭВМ они часто позволяют решить ЗК с n = 100. Это огромный прогресс по сравнению с полным перебором. Кроме того, алгоритмы типа ветвей и границ являются, если нет возможности доводить их до конца, эффективными эвристическими процедурами.
Алгоритм Дейкстры
Одним из вариантов решения ЗК является вариант нахождения кратчайшей цепи, содержащей все города. Затем полученная цепь дополняется начальным городом – получается искомый тур[4: с. 144].
Можно предложить много процедур решения этой задачи, например, физическое моделирование. На плоской доске рисуется карта местности, в города, лежащие на развилке дорог, вбиваются гвозди, на каждый гвоздь надевается кольцо, дороги укладываются верёвками, которые привязываются к соответствующим кольцам. Чтобы найти кратчайшее расстояние между i и k, нужно взять I в одну руку и k в другую и растянуть. Те верёвки, которые натянутся и не дадут разводить руки шире и образуют кратчайший путь между i и k. Однако математическая процедура, которая промоделирует эту физическую, выглядит очень сложно. Известны алгоритмы попроще. Один из них – алгоритм Дейкстры, предложенный Дейкстрой ещё в 1959г. Этот алгоритм решает общую задачу:
В ориентированной, неориентированной или смешанной (т. е. такой, где часть дорог имеет одностороннее движение) сети найти кратчайший путь между двумя заданными вершинами.
Алгоритм использует три массива из n чисел каждый. Первый массив a содержит метки с двумя значениями: 0 (вершина ещё не рассмотрена) и 1 (вершина уже рассмотрена); второй массив b содержит расстояния – текущие кратчайшие расстояния от vi до соответствующей вершины; третий массив c содержит номера вершин – k-й элемент ck есть номер предпоследней вершины на текущем кратчайшем пути из vi в vk. Матрица расстояний Dik задаёт длины дуг dik; если такой дуги нет, то dik присваивается большое число Б, равное «машинной бесконечности».
Последнее изменение этой страницы: 2016-07-22
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...