
Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
Визначення маси і густини Землі.
За законом всесвітнього тяжіння сила взаємодії двох мас 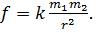 Якщо відома сила
Якщо відома сила  , з якою взаємодіють дві маси, і величина
, з якою взаємодіють дві маси, і величина  однієї з цих мас, то, знаючи відстань
однієї з цих мас, то, знаючи відстань 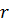 між центрами мас, можна визначити величину
між центрами мас, можна визначити величину  другої маси за формулою
другої маси за формулою  Кулька, масаякої
Кулька, масаякої 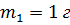 , притягається до Землі з силою
, притягається до Землі з силою  . Відстань між центром кульки й центром Землі дорівнює приблизно
. Відстань між центром кульки й центром Землі дорівнює приблизно  а
а 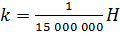 , отже ми можемо обчислити масу Землі
, отже ми можемо обчислити масу Землі 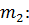

А через те, що об'єм Землі  становить
становить  , то густина Землі
, то густина Землі 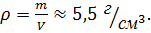
49. Залежність прискорення 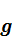 від широти місця.
від широти місця.
Сила тяжіння є окремий випадок всесвітнього тяжіння. Якщо маса будь якого тіла 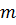 то, позначаючи масу Землі буквою
то, позначаючи масу Землі буквою  і радіус Землі буквою
і радіус Землі буквою  , ми можемо визначити, з якою силою
, ми можемо визначити, з якою силою  дане тіло притягається Землею :
дане тіло притягається Землею :

Сила  є вага тіла
є вага тіла 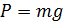 , то:
, то:
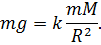
звідки:
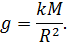
Прискорення сили тяжіння обернено пропорційне до квадрата відстані від центра Землі.
Якщо тіло підноситься над Землею, то відстань від центра Землі збільшується, і величина  зменшується. При піднятті на висоту Ейфелевої башти (300 м) величина
зменшується. При піднятті на висоту Ейфелевої башти (300 м) величина  зменшиться на
зменшиться на 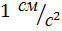 .
.
А через те, що Земля не є геометрична куля, а формою близька до сплющеного еліпсоїда, при чому біля полюсів відстань від центра Землі до рівня моря становить 6357 км, на екваторі 6378 км то величина  змінюється відповідно до широти. На екваторі
змінюється відповідно до широти. На екваторі  менше, ніж біля полюсів.
менше, ніж біля полюсів.
Наслідком обертання Землі навколо осі на всі тіла, що є на Землі, діє відцентрова сила, спричинювана цим обертанням. Величина відцентрового прискорення 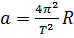 пропорціональна радіусові. Місця земної поверхні, що лежать на різних широтах, неоднаково віддалені від осі обертання Землі; наслідком цього відцентрове прискорення збільшується від полюсів (де воно дорівнює нулеві) до екватора, де воно становить
пропорціональна радіусові. Місця земної поверхні, що лежать на різних широтах, неоднаково віддалені від осі обертання Землі; наслідком цього відцентрове прискорення збільшується від полюсів (де воно дорівнює нулеві) до екватора, де воно становить 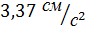 .
.
|
 Отож, прискорення тіла, що падає на екваторі, має бути менше, ніж тіла, що падає на полюсах, на
Отож, прискорення тіла, що падає на екваторі, має бути менше, ніж тіла, що падає на полюсах, на 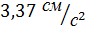 . Наслідком цього прискорення
. Наслідком цього прискорення  зменшується від полюсів до екватора. Значення прискорення
зменшується від полюсів до екватора. Значення прискорення  на рівні моря на полюсі
на рівні моря на полюсі  , на екваторі
, на екваторі  .
.
За нормальне прискорення умовно вважаємо прискорення вільного падання тіла, що дорівнює 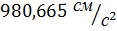 . Одиниця сили 1 кг є сила, з якою Земля притягує масу в 1 кг й надає їй нормальне прискорення
. Одиниця сили 1 кг є сила, з якою Земля притягує масу в 1 кг й надає їй нормальне прискорення 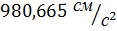 .
.
За законом всесвітнього тяжіння сила ваги має бути напрямлена до центра Землі. Відцентрова сила, що виникає при обертанні Землі і що її напрям тільки на екваторі зливається з напрямом радіуса Землі, трохи відхиляє напрям сили, що діє на тіла біля поверхні Землі.
На полюсах і на екваторі відхилення дорівнює 0. На широті  воно становить
воно становить 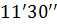 .
.
Напрям рівнодійної сили тяжіння і відцентрової сили називають вертикальним напрямом і визначають виском.
Запитання та вправи
1. У чому суть закону всесвітнього тяжіння?
2. Що називають гравітаційною сталою?
3. Яка величина гравітаційної сталої і що вона означає?
4. Яким дослідом визначено гравітаційну сталу ?
5. З якою силою притягаються одна до одної дві свинцеві кулі, радіуси яких 5 см, якщо від відстань між ними 0,3 см (Густина свинцю 11,3).
6. Як визначають масу Землі?
7. Жоллі, щоб визначити залежність сили притягання від відстані, злагодив терези з двома парами шальок (рис. 46). Одна пара шальок висіла на 5 м нижче другої пари. Зрівноваживши вантажі на верхніх шальках, Жоллі один з вантажів переносив на нижню шальку, при чому терези виходили з рівноваги. З'ясувати чому терези виходили з рівноваги. Яка шалька переважувала?
8. Визначити масу Сонця за такими даними: маса Землі 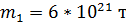 , відстань Землі від Сонця
, відстань Землі від Сонця 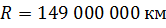 і період обігу Землі навколо Сонця — 1 рік.
і період обігу Землі навколо Сонця — 1 рік.
9. З якою швидкістю треба кинути снаряд в горизонтальному напрямі, щоб він не впав на Землю, а почав оббігати навколо Землі колом? (На опір повітря не зважати).
VI. СТАТИКА
Графічне зображення сил.
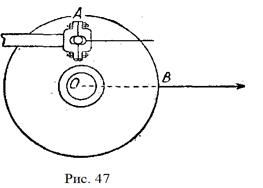 Сили, що діють на тіло, можуть відрізнятися одна від одної і величиною, і напрямом. Штовхаючи з більшою чи меншою силою футболь ний м'яч, ми надаємо йому більшої або меншої швидкості. Залежно від напряму діючої сили футбольний м'яч летить у тому чи іншому напрямі. Має також значення точка прикладання сили — точка тіла, на яку діє сила. Справді, якщо ми прив'яжемо мотузку в точці
Сили, що діють на тіло, можуть відрізнятися одна від одної і величиною, і напрямом. Штовхаючи з більшою чи меншою силою футболь ний м'яч, ми надаємо йому більшої або меншої швидкості. Залежно від напряму діючої сили футбольний м'яч летить у тому чи іншому напрямі. Має також значення точка прикладання сили — точка тіла, на яку діє сила. Справді, якщо ми прив'яжемо мотузку в точці  маховика (рис. 47) і натягатимемо її в напрямі
маховика (рис. 47) і натягатимемо її в напрямі  , то маховик повернеться. Навпаки, якщо ми прив'яжемо мотузку в точці
, то маховик повернеться. Навпаки, якщо ми прив'яжемо мотузку в точці  і з такою силою тягтимемо її в тому самому напрямі, то такого руху маховика не буде.
і з такою силою тягтимемо її в тому самому напрямі, то такого руху маховика не буде.
Щоб визначити силу, ми повинні знати: 1) величину сили, 2) її напрям, 3) точку її прикладання.
Точку прикладання сили можна перенести в будь-яку точку тіла в напрямі сили. Ми можемо надати руху маховикові, якщо прив'яжемо в точці  довшу мотузку і тягтимемо її за кінець у попередньому напрямі, або прикріпимо до точки
довшу мотузку і тягтимемо її за кінець у попередньому напрямі, або прикріпимо до точки 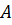 шток і штовхатимемо цей шток у тому таки напрямі
шток і штовхатимемо цей шток у тому таки напрямі 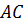 . Паровоз, що тягне поїзд, можна причепити і на початку поїзда, і в його хвості, і всередині, при цьому дія сили не зміниться.
. Паровоз, що тягне поїзд, можна причепити і на початку поїзда, і в його хвості, і всередині, при цьому дія сили не зміниться.
Сили, як векторні величини, зображуються різної величини відрізками прямої з стрілкою на кінці. Починається відрізок у точці прикладання сили (рис. 47).
51. Додавання сил, що діють в напрямі однієї прямої.
Коли на тіло діє яка-небудь одна сила, то воно рухається в напрямі прикладеної сили. Якщо на тіло діє не одна, а дві або кілька сил у різних напрямах, то тіло або залишається в спокої, або набуває руху, який може спричинити одна сила в якомусь цілком певному напрямі.
Сила, що діє на тіло так само, як дві або кілька сил, взятих разом, називається рівнодійною даних сил.
Ті сили, що ми замінюємо рівнодійною силою, називаються складовими.
Відшукання рівнодійної за даними складовими називають додаванням сил.
Розглянемо на прикладі, як додавати сили, що діють на тіло в напрямі однієї прямої.
Приклад 1. Поїзд рухається подвійною тягою. Сила тяги одного з паровозів дорівнює  кг, другого
кг, другого 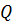 кг. Знайти рівно дійну сил
кг. Знайти рівно дійну сил  і
і 
Розв'язання. Рівнодійна 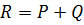 тобто сумі сил складових.
тобто сумі сил складових.
Приклад 2. Камінь, що важить  кг, падає у повітрі. Опір повітря —
кг, падає у повітрі. Опір повітря —  кг. Знайти рівнодійну сил ваги й опору.
кг. Знайти рівнодійну сил ваги й опору.
Розв'язання. Очевидно, у даному разі  — тобто рівнодійна дорівнює різниці сил складових і йде в напрямі більшої сили.
— тобто рівнодійна дорівнює різниці сил складових і йде в напрямі більшої сили.
Рівнодійна двох або кількох сил, що діють на напрямі тієї самої прямої лінії, дорівнює алгебричній сумі сил складових.
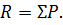
52. Додавання двох сил, прикладених до однієї точки під кутам одна до одної.
Рівнодійна двох сил, прикладених до однієї точки тіла під кутом одна до одної, величиною і напрямом дорівнює діагоналі паралелограма, побудованого на цих силах.
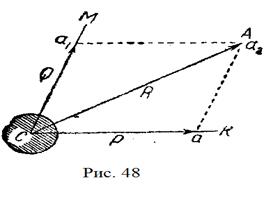
На рис. 48 подано приклад додавання двох сил  і
і 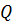 що діють на точку
що діють на точку  тіла під кутом одна до одної. Будуючи на даних силах паралелограм
тіла під кутом одна до одної. Будуючи на даних силах паралелограм  , знайдемо діагональ цього паралелограма
, знайдемо діагональ цього паралелограма  , що й величиною й напрямом відповідає рівнодійній сил
, що й величиною й напрямом відповідає рівнодійній сил  і
і 
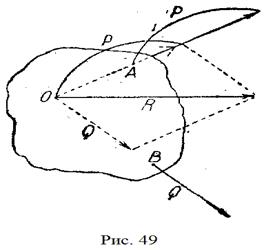
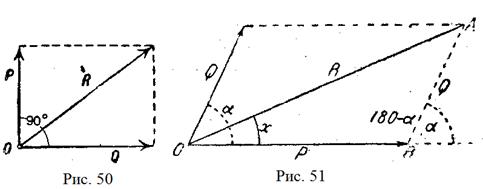
У тому випадку, коли дані сили лежать в одній площині, але прикладені не до однієї точки, а до двох різних точок тіла —  і
і  (рис. 49), ми визначимо рівнодійну сил таким способом. Продовжуючи напрями даних сил, знайдемо точку
(рис. 49), ми визначимо рівнодійну сил таким способом. Продовжуючи напрями даних сил, знайдемо точку  , де вони перетинаються. Переносячи в цю точку
, де вони перетинаються. Переносячи в цю точку  точки прикладання сил
точки прикладання сил  і
і 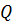 (рис. 51), визначаємо за правилом паралелограма рівнодійну
(рис. 51), визначаємо за правилом паралелограма рівнодійну 
Діагональ паралелограма визначається або графічно за масштабом, або обчисленням за допомогою тригонометрії.
Для найпростішого випадку, коли дві сили  і
і 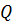 , діють під прямим кутом одна до одної (рис. 50) їхню рівнодійну можна обчислити за теоремою Піфагора.
, діють під прямим кутом одна до одної (рис. 50) їхню рівнодійну можна обчислити за теоремою Піфагора.
 Щоб обчислити величину сили в загальному виді, треба застосувати теорему з тригонометрії: квадрат сторони трикутника дорівнює сумі квадратів двох інших сторін без подвоєного добутку цих сторін на косинус кута між ними.
Щоб обчислити величину сили в загальному виді, треба застосувати теорему з тригонометрії: квадрат сторони трикутника дорівнює сумі квадратів двох інших сторін без подвоєного добутку цих сторін на косинус кута між ними.
Позначивши кут між силами  і
і 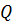 (рис. 51) буквою
(рис. 51) буквою  , з трикутника
, з трикутника  дістанемо:
дістанемо: 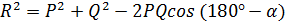 , але
, але  . Через це
. Через це
 .
.
В окремому випадку, коли сили напрямлені в один бік, то
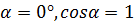
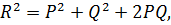
тобто:
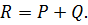
Якщо сили  і
і 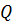 розміщені під кутом 90°, то
розміщені під кутом 90°, то
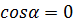
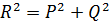
Якщо сили напрямлені протилежно, то 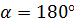 ,
,


звідси:

Щоб визначити напрям рівнодійної сили, застосуємо до трикутника  теорему: сторони трикутника пропорційні синусам протилежних кутів. Позначивши кут між силами
теорему: сторони трикутника пропорційні синусам протилежних кутів. Позначивши кут між силами  і
і 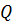 буквою
буквою 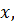 дістанемо:
дістанемо:

але  ; через це:
; через це:
 . .
. .
Отже, рівнодійна визначена і величиною, і напрямом.
Приклад 1. Дано дві сили:  кг і
кг і  4 кг, що діють під прямим кутом. Знайти рівнодійну.
4 кг, що діють під прямим кутом. Знайти рівнодійну.
Розв'язання. Будуємо паралелограм сил, що на цей раз є прямокутник, і обчислюємо  за теоремою Піфагора:
за теоремою Піфагора:
 кг.
кг.
Вправа.
1. Нарисувати такий випадок додавання двох сил під кутом, коли рівнодійна де менша за кожну із складових.
2. Між якими границями змінюється рівнодійна двох сил  і
і 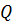 , прикладених до точки під кутом, залежно від величини кута.
, прикладених до точки під кутом, залежно від величини кута.
Додавання кількох сил.
У техніці рідко мають справу тільки з двома силами. Різні частини споруд зазнають дії кількох сил у найрізноманітніших напрямах. Нехай на точку  (рис. 52) діють не дві сили, а більше, наприклад, 4 сили:
(рис. 52) діють не дві сили, а більше, наприклад, 4 сили:  що лежать в одній площині.
що лежать в одній площині.
|
|
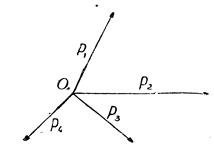

Щоб знайти рівнодійну, треба додавати сили поступово. Тай спочатку додаємо  за правилом паралелограма (рис. 53); дістанемо їх рівнодійну
за правилом паралелограма (рис. 53); дістанемо їх рівнодійну  , далі додаємо до добутої сили дальшу складову
, далі додаємо до добутої сили дальшу складову 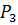 ; маємо рівнодійну
; маємо рівнодійну 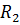 . Будуємо паралелограм на силах
. Будуємо паралелограм на силах 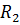 і
і  ; знаходимо остаточно
; знаходимо остаточно 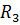 , що буде шуканою рівнодійною чотирьох даних сил:
, що буде шуканою рівнодійною чотирьох даних сил:  .
.
|
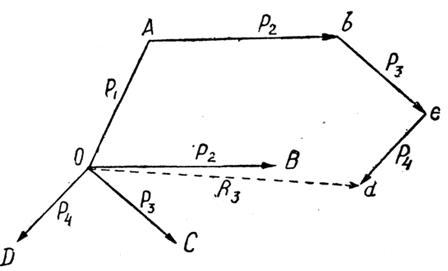
Із рис. 53 і 54 бачимо, що для знаходження рівнодійної 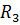 можна і не малювати паралелограмів
можна і не малювати паралелограмів  і т. д. Досить з кінця відрізка
і т. д. Досить з кінця відрізка  провести відрізок
провести відрізок  , рівний і паралельний до
, рівний і паралельний до  ; і з кінця
; і з кінця  провести
провести 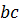 рівний і паралельний до
рівний і паралельний до 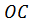 і т. д. Відрізок
і т. д. Відрізок 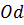 , що є замикаюча сторона многокутника
, що є замикаюча сторона многокутника  побудованого на складових силах, і дасть рівнодійну цих сил.
побудованого на складових силах, і дасть рівнодійну цих сил.
Вправа.
1. Довести, що рівнодійна трьох рівних сил, напрямлених під кутом  одна до,одної, дорівнює нулеві.
одна до,одної, дорівнює нулеві.
Зрівноважувальна сила.
Зробимо дослід, показаний на рис. 55. До двох динамометрів, що висять на гачках, прив'яжемо нитку, і через неї в точці 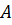 перекинемо гачок з гирею.
перекинемо гачок з гирею.
|
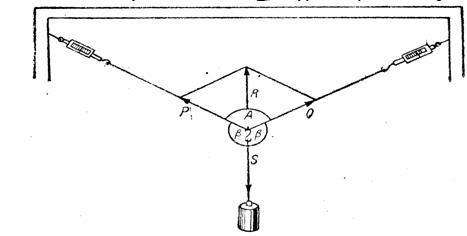
На точку 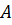 діють 3 сили: дві пружини динамометрів тягнуть точку
діють 3 сили: дві пружини динамометрів тягнуть точку 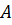 вгору, а вага гирі тягне її вниз. Точка
вгору, а вага гирі тягне її вниз. Точка 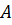 перебував в рівновазі.
перебував в рівновазі.
Вага гирі 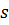 зрівноважує натяг динамометрів
зрівноважує натяг динамометрів  і
і 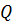 . Тому в даному прикладі силу
. Тому в даному прикладі силу 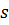 називають зрівноважувальною силою, а сили
називають зрівноважувальною силою, а сили  і
і 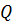 називають, як і раніше, складовими силами. Додавши їх за правилом паралелограма, матимемо діагональ що відповідає рівнодійній сил
називають, як і раніше, складовими силами. Додавши їх за правилом паралелограма, матимемо діагональ що відповідає рівнодійній сил  і
і 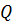 .
.
Напрям вектора  прямо протилежний напрямові зрівноважувальної сили
прямо протилежний напрямові зрівноважувальної сили 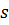 і величиною вектор
і величиною вектор  дорівнює векторові
дорівнює векторові 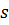 , Інакше ми не мали б рівноваги.
, Інакше ми не мали б рівноваги.
Отже, зрівноважувальна двох даних сил величиною дорівнює рівнодійній цих сил і напрямом прямо протилежна їй.
Отже, ми можемо знайти рівнодійну двох або кількох сил, якщо відома зрівноважувальна сила.
Для цього треба провести вектор протилежно зрівноважувальній силі і відкласти на ньому її величину.
Розклад сил.
Як дві сили, що діють на тіло під кутом одна до одної, можна замінити однією рівнодійною, так само одну силу, що діє на тіло, можна замінити двома або кількома силами, що так само діють, як і дана сила.
 Хлопчик везе санки, натягаючи мотузку під кутом
Хлопчик везе санки, натягаючи мотузку під кутом  до горизонту (рис. 56). Санки рухаються не в напрямі прикладеної сили. Сила натягу мотузки розкладається на дві сили. Одна з цих сил напрямлена горизонтально і надає руху санкам, а друга напрямлена догори і підіймає передню частину санок.
до горизонту (рис. 56). Санки рухаються не в напрямі прикладеної сили. Сила натягу мотузки розкладається на дві сили. Одна з цих сил напрямлена горизонтально і надає руху санкам, а друга напрямлена догори і підіймає передню частину санок.
У даному випадку, щоб розкласти сили, ми скористувалися правилом паралелограма, тільки дану силу ми вважали за діагональ паралелограма, а шукані сили — за сторони паралелограма.
Очевидно, питання розкладу сил на складові є питання неозначене, тому, що на одній діагоналі можна побудувати скільки завгодно різних паралелограмів. Тому в кожному випадку розкладу сил спочатку ніж будувати паралелограм, треба визначити, як мають бути напрямлені шукані сили, або яка повинна бути їх величина. Розглянемо ці питання на кількох прикладах.
Приклади розкладу сил.
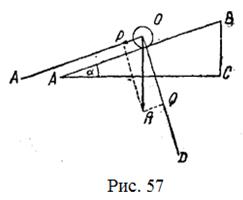 1. Похила площина. По похило поставлених дошках викочують вгору важку бочку (рис. 57). Вага бочки
1. Похила площина. По похило поставлених дошках викочують вгору важку бочку (рис. 57). Вага бочки  на похилій площині розкладається на дві сили. Одна сила скочує бочку по похилій площині; вона напрямлена вздовж цієї площини. Друга сила притискує бочку до похилої площини; вона напрямлена перпендикулярно до цієї площини. Щоб знайти величину сил, на які розкладається вага бочки
на похилій площині розкладається на дві сили. Одна сила скочує бочку по похилій площині; вона напрямлена вздовж цієї площини. Друга сила притискує бочку до похилої площини; вона напрямлена перпендикулярно до цієї площини. Щоб знайти величину сил, на які розкладається вага бочки  , треба побудувати паралелограм, одна сторона якого напрямлена паралельно з похилою площиною, а друга сторона — перпендикулярна до похилої площини. З точки
, треба побудувати паралелограм, одна сторона якого напрямлена паралельно з похилою площиною, а друга сторона — перпендикулярна до похилої площини. З точки  проводимо лінію
проводимо лінію  , паралельну з
, паралельну з  і лінію
і лінію 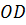 перпендикулярну до
перпендикулярну до  (рис. 57).
(рис. 57).
З точки  проводимо лінії паралельні з
проводимо лінії паралельні з  і
і 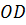 , тобто доповнюємо фігуру до паралелограма. Маємо вектори
, тобто доповнюємо фігуру до паралелограма. Маємо вектори 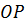 і
і 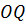 , на які ми розкладали вагу тіла на похилій площині. Робітникам треба зрівноважити силу
, на які ми розкладали вагу тіла на похилій площині. Робітникам треба зрівноважити силу 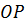 і тоді бочка не скотиться вниз. Сила
і тоді бочка не скотиться вниз. Сила 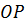 менша від ваги
менша від ваги  отже, з допомогою похилої площини ми виграємо в силі.
отже, з допомогою похилої площини ми виграємо в силі.
Відшукаємо залежність вектора 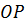 від вектора
від вектора  . Трикутники
. Трикутники 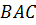 і
і  подібні, вони прямокутні і, крім того, кути
подібні, вони прямокутні і, крім того, кути 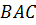 і
і  утворені взаємно перпендикулярними сторонами; із подібності трикутників маємо:
утворені взаємно перпендикулярними сторонами; із подібності трикутників маємо:
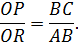
Звідси:
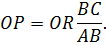
Але відношення  синусу кута нахилу
синусу кута нахилу  а тому остаточно
а тому остаточно  , тобто сила, напрямлена вздовж похилої площини, дорівнює вазі тіла, помноженій на синус кута нахилу.
, тобто сила, напрямлена вздовж похилої площини, дорівнює вазі тіла, помноженій на синус кута нахилу.
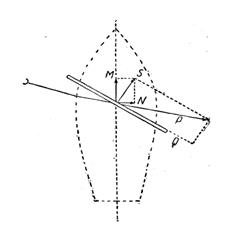
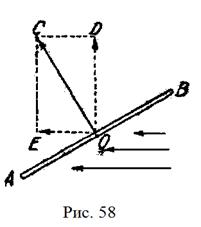 2. Паперовий змій. Лінія
2. Паперовий змій. Лінія  (рис. 58) є площина паперового змія. Покажемо, що під час вітру утворюється підіймальна сила. Ми знаємо, що вітер тисне на поверхню змія. Сила тиску перпендикулярна до поверхні змія. Отже, сила тиску вітру на поверхню змія е вектор
(рис. 58) є площина паперового змія. Покажемо, що під час вітру утворюється підіймальна сила. Ми знаємо, що вітер тисне на поверхню змія. Сила тиску перпендикулярна до поверхні змія. Отже, сила тиску вітру на поверхню змія е вектор 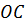 . Розкладемо його на два складові вектори:
. Розкладемо його на два складові вектори: 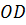 і
і 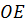 . З них вектор
. З них вектор 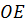 є опір змія вітрові, а вектор
є опір змія вітрові, а вектор 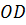 — підіймальна сила. Сила
— підіймальна сила. Сила 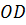 тільки частково врівноважується вагою змія, решту йде на підіймання.
тільки частково врівноважується вагою змія, решту йде на підіймання.
|
 3. Крило літака. Таким же способом утворюється підіймальна сила на крилах літака (рис. 59). Відмінність від змія тут у тому, що вітер утворюється тягою самого літака. Тиск повітря на крила літака, що рухається, зображено вектором
3. Крило літака. Таким же способом утворюється підіймальна сила на крилах літака (рис. 59). Відмінність від змія тут у тому, що вітер утворюється тягою самого літака. Тиск повітря на крила літака, що рухається, зображено вектором 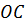 . Розкладаючи його за правилом паралелограма, ми дістанемо два складові вектори:
. Розкладаючи його за правилом паралелограма, ми дістанемо два складові вектори: 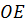 — так званий лобовий опір і
— так званий лобовий опір і 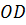 – підіймальну силу. При певному нахилі крил літака (кут атаки) і належній швидкості руху утворюється достатня підіймальна сила, наслідком чого літак під час руху тримається в повітрі і не падає.
– підіймальну силу. При певному нахилі крил літака (кут атаки) і належній швидкості руху утворюється достатня підіймальна сила, наслідком чого літак під час руху тримається в повітрі і не падає.
|
 . Розкладемо цей вектор за правилом паралелограма на вектор
. Розкладемо цей вектор за правилом паралелограма на вектор 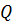 , що ковзає вздовж вітрила, і вектор
, що ковзає вздовж вітрила, і вектор 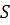 , перпендикулярний до поверхні вітрила. Вектор
, перпендикулярний до поверхні вітрила. Вектор 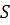 є сила тиску вітру на вітрило. Розкладаючи вектор
є сила тиску вітру на вітрило. Розкладаючи вектор 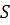 на два напрями, один з яких іде вздовж кіля човна, і другий, йому перпендикулярний, відшукуємо силу
на два напрями, один з яких іде вздовж кіля човна, і другий, йому перпендикулярний, відшукуємо силу 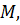 що рухає човен вперед, і силу
що рухає човен вперед, і силу 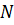 , що тисне на човен збоку. Вітер діє на вітрило човна з силою
, що тисне на човен збоку. Вітер діє на вітрило човна з силою  , а човен рухається в напрямі
, а човен рухається в напрямі  .
.
Вправи.
1. На двох однакових завдовжки тросах висить тягар 50 кг. Кут між трасами  . Знайти сили, що тримають тягар.
. Знайти сили, що тримають тягар.
2. Визначити сили, що тримають тягар 50 кг, якщо кут між рівними довжиною тросами дорівнює: а) 45  ; б) 120
; б) 120  ; в)
; в)  .
.
3. Чи може бути такий випадок, що рівнодійна дорівнює 30 кг, а дві складові сили — по 10 кг кожна.
Додавання паралельних сил.
Нехай ми маємо дві паралельні сили  і
і 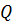 , напрямлені в один бік і прикладені до тіла в точках
, напрямлені в один бік і прикладені до тіла в точках 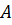 і
і  (рис. 61). Треба знайти їх рівнодійну силу (тобто визначити її напрям, величину і точку прикладання).
(рис. 61). Треба знайти їх рівнодійну силу (тобто визначити її напрям, величину і точку прикладання).
|
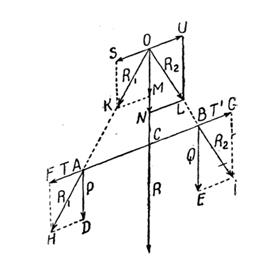 Щоб розв'язати цю задачу, зробимо допоміжну побудову. Сполучаємо точки
Щоб розв'язати цю задачу, зробимо допоміжну побудову. Сполучаємо точки  і
і  і прикладаємо в напрямі
і прикладаємо в напрямі  , ліворуч від точки
, ліворуч від точки  іправоруч від точки
іправоруч від точки  , рівні й протилежні сили
, рівні й протилежні сили  і
і 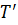 . Від додавання цих сил дія сил
. Від додавання цих сил дія сил  і
і 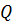 на тіло не зміниться. Додаємо вектори
на тіло не зміниться. Додаємо вектори 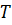 і
і  , а також
, а також 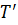 і
і 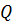 за правилом паралелограма; дістанемо рівнодійні
за правилом паралелограма; дістанемо рівнодійні 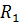 і
і 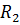 . Продовжимо діагоналі паралелограмів до перетину в точці
. Продовжимо діагоналі паралелограмів до перетину в точці  . Перенесемо точки прикладання сил
. Перенесемо точки прикладання сил 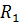 і
і 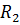 у точку
у точку  . Від цього переносу дія сил на тіло також не зміниться, тому, що ми переносимо і
. Від цього переносу дія сил на тіло також не зміниться, тому, що ми переносимо і 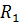 і
і 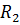 в напрямі сил. У точці
в напрямі сил. У точці 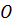 знову розкладаємо
знову розкладаємо 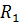 і
і 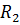 на складові. Паралелограм
на складові. Паралелограм  дорівнює паралелограмові
дорівнює паралелограмові 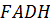 . Паралелограм
. Паралелограм 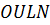 дорівнює паралелограмові
дорівнює паралелограмові  . Вектор
. Вектор 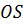 дорівнює вектору
дорівнює вектору 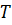 , вектор
, вектор 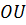 дорівнює вектору
дорівнює вектору 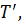 дії
дії 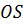 і
і 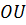 взаємно зрівноважуються, вектор
взаємно зрівноважуються, вектор  дорівнює вектору P, а
дорівнює вектору P, а 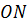 — вектору
— вектору 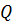 ; дія їх додається і дає рівнодійну
; дія їх додається і дає рівнодійну  , що дорівнює сумі
, що дорівнює сумі  .
.
Отже, рівнодійна  двох паралельних сил
двох паралельних сил  і
і 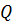 дорівнює їх сумі і напрямлена паралельно з даними силами. Точку її прикладання переносимо в
дорівнює їх сумі і напрямлена паралельно з даними силами. Точку її прикладання переносимо в  . Із подібності трикутників
. Із подібності трикутників 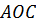 і
і  напишемо:
напишемо:
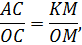
а з подібності трикутників  і
і  маємо:
маємо:
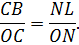
Поділивши одну пропорцію на другу і відзначивши, що  , дістанемо:
, дістанемо:  Але
Але 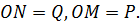 Підставивши ці значення в написану пропорцію, отримаємо остаточно:
Підставивши ці значення в написану пропорцію, отримаємо остаточно:
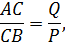
тобто точка прикладання рівнодійної паралельних сил  і
і 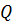 лежить від точок
лежить від точок 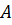 і
і  на відстанях, обернено пропорційних складовим силам
на відстанях, обернено пропорційних складовим силам  і
і 
Вправи.
5. Терези зрівноважені. Вага кожної шальки і важка по 2 кг. Довжина коромисла терезів 40 см. Подати графічно сили й плечі, показавши складові сили і зрівноважувальну силу (опір підставки).
6. Дано паралельні сили: 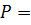 40 кг,
40 кг,  = 60 кг. Відстань між ними дорівнює 50 см. Побудувати у відповідному масштабі рівнодійну.
= 60 кг. Відстань між ними дорівнює 50 см. Побудувати у відповідному масштабі рівнодійну.
7. На кінцях стрижня завдовжки 1 м є тягарі на 80 кг і 20 кг. Визначити, в якому місці треба підперти стрижень, щоб мати рівновагу. Розв'язати задачу обчисленням і побудувати сили на папері
8. Дано паралельні сили:  = 100 кг,
= 100 кг, 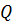 = 300 кг, відстань між ними 40 см. Визначити рівнодійну і точку її прикладання. Розв'язати обчисленням і побудувати графічно.
= 300 кг, відстань між ними 40 см. Визначити рівнодійну і точку її прикладання. Розв'язати обчисленням і побудувати графічно.
Последнее изменение этой страницы: 2016-07-23
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...